Отрезок :: Компания "Аякс" Томск

19.02.2016 09:00

Отре́зком называются два близких понятия: в геометрии и математическом анализе.

Содержание

Отрезок в геометрии

Отрезок прямой — часть прямой, ограниченная двумя точками. Точнее: это множество, состоящее из двух различных точек данной прямой (которые называются концами отрезка) и всех точек, лежащих между ними (которые называются его внутренними точками). Отрезок, концами которого являются точки $\;A$ и $\;B$ , обозначается символом $AB$ . Расстояние между концами отрезка называют его длиной и обозначают $|AB|$ .

Направленный отрезок

Основная статья: Вектор (математика)

Обычно у отрезка прямой неважно, в каком порядке рассматриваются его концы: то есть отрезки $AB$ и $BA$ представляют собой один и тот же отрезок. Если у отрезка определить направление, то есть порядок перечисления его концов, то такой отрезок называется направленным. Например, направленные отрезки $AB$ и $BA$ не совпадают. Особого обозначения у направленных отрезков нет — то, что у отрезка важно его направление обычно указывается особо.

Дальнейшее обобщение приводит к понятию вектора — класса всех равных по длине и сонаправленных направленных отрезков.

Отрезок числовой прямой

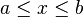Отрезок числовой (координатной) прямой (иначе числовой отрезок, сегмент) — множество вещественных чисел $\{x\}~$ , удовлетворяющих неравенству $a \le x \le b$ , где заранее заданные вещественные числа $a~$ и $b~$ $(a<b)~$ называются концами (граничными точками) отрезка. В противоположность им, остальные числа $x~$ , удовлетворяющие неравенству $a<x<b~$ , называются внутренними точками отрезка^[1].

Отрезок обычно обозначается $[a, b]$ :

[a,b] = \{ x \in \mathbb{R} \mid a \le x \le b \}

Любой отрезок, по определению, заведомо включён в множество вещественных чисел. Отрезок является замкнутым промежутком.

Число 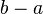$b-a\,$ называется длиной числового отрезка $[a, b]$ .

Стягивающаяся система сегментов

Система сегментов — это бесконечная последовательность элементов множества отрезков на числовой прямой $\{[a, b] | a, b \in \R \land a < b\}$ .

Система сегментов обозначается $\{[a_n, b_n]\}_{n = 1}^{\infty}$ . Подразумевается, что каждому натуральному числу $~n$ поставлен в соответствие отрезок $~[a_n, b_n]$ .

Система сегментов $\{[a_n, b_n]\}_{n = 1}^{\infty}$ называется стягивающейся, если^[2]

каждый следующий отрезок содержится в предыдущем;

$\forall n \in \N \colon [a_{n+1}, b_{n+1}] \subseteq [a_n, b_n]$
соответствующая последовательность длин отрезков бесконечно мала.

$\lim_{n \to \infty} (b_n - a_n) = 0$

У любой стягивающейся системы сегментов существует единственная точка, принадлежащая всем сегментам этой системы.

\forall \{[a_n, b_n]\}_{n = 1}^{\infty} ~ \exists ! c \in \R ~ \forall n \in N \colon c \in [a_n, b_n]

Этот факт следует из свойств монотонной последовательности.